高分子流体のマルチスケールシミュレーション
身の周りに多くの高分子製品が存在することからも分かるように、現在の我々の生活において高分子はなくてはならないものとなっています。このような高分子製品は、成形加工の段階で高分子流体として扱われます。そのため、その流動を正確に予測・制御することが重要であることは想像に難くありません。
高分子流体の特徴としては、時空間的に高い階層構造を持つことがよく知られています。この階層構造を念頭に置くと、高分子鎖の「ミクロレベルの構造や状態」を出発点とし、狙った物性を有する高分子製品を設計することは、化学工学・物質科学などの分野における大きな目標の1つです。
上述のような特徴を持つ高分子流体の流動挙動を正確に予測・制御し、また高分子鎖レベルの情報を製品設計の変数として取り入れるためには、マクロレベルの流動に着目するだけでなくミクロレベルの高分子鎖の状態を理解することが必要です。計算科学の分野では、このような異なるスケール間の関係を詳しく扱う手法として、異なるスケール間のモデルを相互に連携して計算を行うマルチスケールシミュレーション(MSS)法の確立が強く望まれています。
このような問題に対して我々は、マクロレベルの流体モデルと、ミクロレベルの粗視化高分子モデルを組み合わせて流動予測を行うMSS法を開発しました。開発したMSS法について、高分子の繊維を製造するプロセスを単純化した問題や、急縮小・急拡大流路における流動問題に対してテストを行いました。
- Takeshi Sato, Kohei Harada, and Takashi Taniguchi*, "Multiscale Simulations of Flows of a Well-Entangled Polymer Melt in a Contraction–Expansion Channel", Macromolecules, 52, 547-564 (2019).
- Takeshi Sato and Takashi Taniguchi*, "Multiscale simulations for entangled polymer melt spinning process", J. Non-Newtonean Fluid Mech., 241, 34-42 (2017).
ひも状ミセル溶液の粗視化モデル
日常生活における消費剤等の用途として用いられる界面活性剤溶液は、その濃度や添加する塩の濃度等のパラメータに応じていくつかの異なる自己組織化構造を形成することが知られています。ひも状ミセルはそれらの自己組織化構造の1つであり、からみあい状態にある高分子溶液とよく似たレオロジー特性を示します。工学的な応用の観点から、上記のようなひも状ミセルが示す顕著な粘弾性的性質の起源を理解することは重要です。
ひずみの小さい線形領域の粘弾性的性質は、過去の研究によって比較的よく理解されています。一方で、非線形粘弾性挙動については線形粘弾性に比べて理解が進んでいません。これは、からみあいに由来する「高分子らしさ」に加えて、ミセルの分裂と結合の機構を構成方程式に組み込むことの困難さに起因します。多くの既往の研究では、高分子溶液のレオロジー予測に用いられるモデルをひも状ミセル溶液の系に適用し、経験的に非線形の流動の予測を行っています。しかしこの手法には、紐状ミセルにおける分裂と結合が考慮されておらず、流動の分子論的な特徴付けが困難です。
このような背景から、ひも状ミセル溶液の非線形のレオロジー挙動を予測するための粗視化モデルの開発することは,基礎科学においても重要な課題と言えます。そこで、からみあい状態にある高分子のダイナミクスを予測するためのモデルに分裂と結合の機構を組み込むことで、ひも状ミセル溶液のレオロジー予測に拡張することを試みました。
関連論文:- Takeshi Sato, Soroush Moghadam, Grace Tan, Ronald G. Larson*, "A slip-spring simulation model for predicting linear and nonlinear rheology of entangled wormlike micellar solutions", J. Rheol., 64, 1045-1061 (2020).
- Takeshi Sato and Ronald G. Larson*, "Nonlinear Rheology of Entangled Wormlike Micellar Solutions Predicted by A Micelle-Slip-Spring Model", J. Rheol., 66, 639-656 (2022).
高分子流体の構成方程式
変形(および変形の速度)と応力を結びつける式を構成方程式と呼びます。これまでの研究で、高分子の分子量(絡み合い? or 非絡み合い?)や高分子の構造(線状高分子? or 分岐高分子?)などに依存して数多くの構成方程式が提案されています。
特に非絡み合いの線状高分子については、Rouseモデルと呼ばれるモデルが有名です。Rouseモデルは非絡み合い高分子の線形粘弾性データを見事に記述しますが、せん断や伸長流動下などの非線形粘弾性データに対しては実験結果と食い違いが見られます。この食い違いに対して、バネの伸び切り効果の重要性が過去の研究において重要とされてきました。最近の研究結果から、流動下での摩擦の低下やブラウン運動の強度の変化についても着目されています。以上の非線形パラメータを含む構成方程式の導出を行いました。
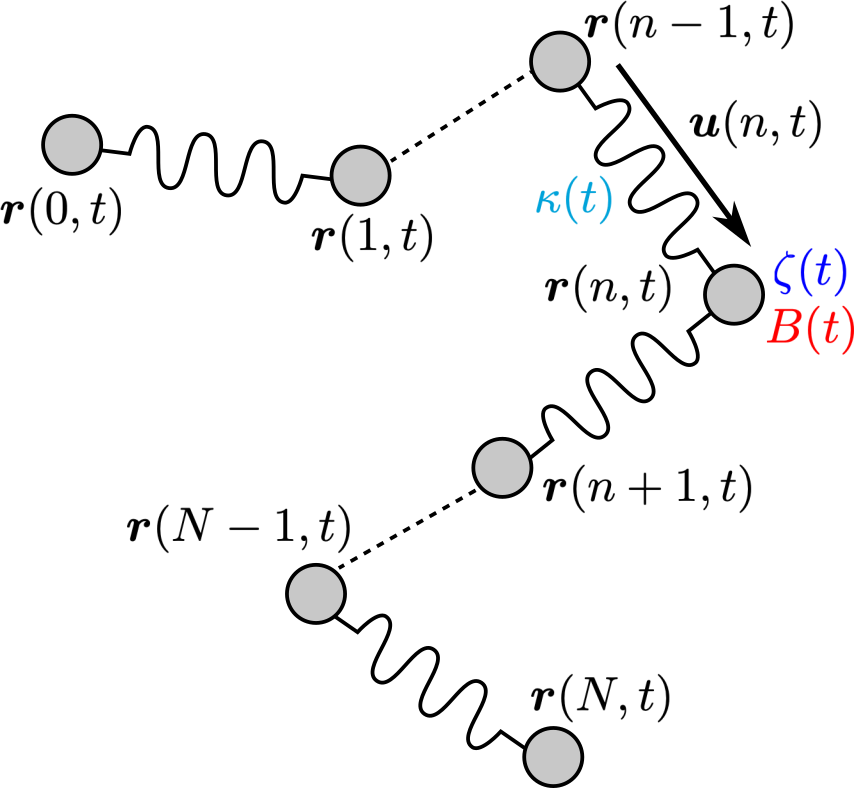
- Takeshi Sato, Youngdon Kwon, Yumi Matsumiya, and Hiroshi Watanabe*, "A Constitutive Equation for Rouse Model Modified for Variations of Spring Stiffness, Bead Friction, and Brownian Force Intensity Under Flow", Phys. Fluids, 33, 063106 (2021).
高分子ブレンドの相分離ダイナミクス
under construction.

